Image Registration using Control Points

License Javadocs Quality Gate Status codecov Maven Central

TL;DR;

Image registration is the process of finding the transform to match a given image with a desired reference. This library supports rigid body transforms (translation and rotation) as well as affine transforms (anisotropic scaling, anisotropic rotation/shear aka. non-orthogonality). Currently non-linear transforms are not supported.

Version 0.0.5 will introduce a method to select different linear algebra frameworks to be used in image-registration. Here it will be possible to choose either gov.nist.math.jama, org.la4j, org.ejml, org.apache.commons.math3 or even org.jblas. There will be a core or api JAR for image-registration and there will be a group of JARs providing a solver implementation. The solver will be selected using the Java SPI (Service Provider Interface) mechanism.

These methods are used e.g. in photomask manufacturing, medical imaging or geospatial applications. Control point or feature based methods have only limited scope of use in medical imaging, there intensity based or voxel based methods are preferred due to the natural structure of medical image data. These additional intensity and voxel based methods are not supported by this library.

How to start?

The SNAPSHOT-API documentation is available on: https://www.raumzeitfalle.net/image-registration/api/ Version 0.0.5 is available on Maven Central using following snippet:

<dependency>
  <groupId>net.raumzeitfalle.registration</groupId>
  <artifactId>image-registration</artifactId>
  <version>0.0.5</version>
</dependency>
<dependency>
  <groupId>net.raumzeitfalle.registration</groupId>
  <artifactId>solver-api</artifactId>
  <version>0.0.5</version>
</dependency>
<dependency>
  <groupId>net.raumzeitfalle.registration</groupId>
  <artifactId>jama-solver</artifactId>
  <version>0.0.5</version>
</dependency>

The artifact image-registration provides the actual API for image registration using control points. The solver-api artifact defines the service provider interface which is required to integrate different externa linear algebra (LA) libraries. The third artifact in this example, jama-solver provides an implementation to the solver-api based on NIST JAMA library.

When the consumer project requires a different LA library, the appropriate implementation provided by this project can be used. In case a custom implementaton is required, this must be created based on solver-api.

New API structure

Module Purpose
image-registration Image Registration API without any external solver binding
solver-api API to utilize different linear algebra frameworks for calculation

Following solver implementations will be available

Solver Module Dependency to: Library version:
apache-math3-solver org.apache.commons:commons-math3 3.6.1
ejml-solver org.ejml:ejml-simple 0.41
jama-solver gov.nist.math:jama 1.0.3
jblas-solver org.jblas:jblas 1.2.5
la4j-solver org.la4j:la4j 0.6.0

More Linear Algebra libraries:

Goals

Todos

How does is work?

Processing steps

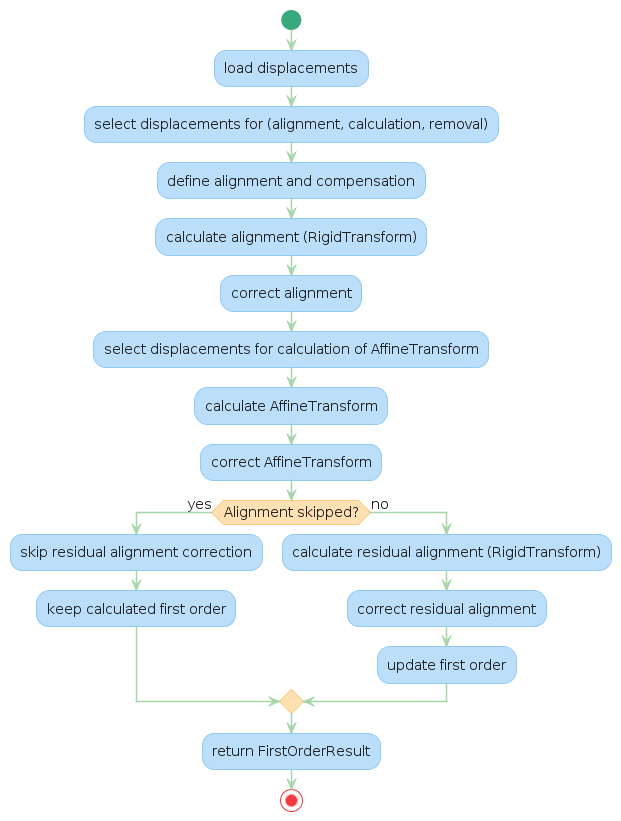
Steps to registration correction

Concepts

Domain types

Interfaces

Transforms

Transforms are used to manipulate displacement elements. Depending on the model used, there may exist different transform types and implementations. Each transform is a Function which, applied to a Displacement, will return a Displacement. There are currently two base transforms, the RigidTransform and the AffineTransform. When transforms are parameterized in a way that there will be actually no change to the displacement data, then in some cases a SkipTransform might be created and used. A SkipTransform must not perform any calculations, instead it must pass through the given data without any modifications.

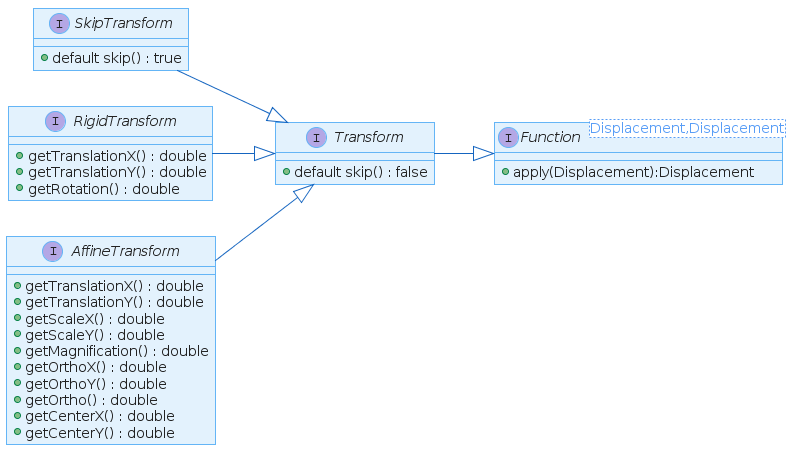
Transforms Interfaces

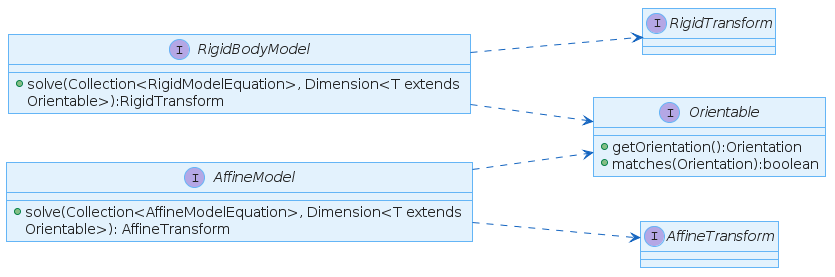
Transform Models

One idea and goal is, to make the underlying transformation models exchangeable. Therefore the RigidBodyModel and the AffineModel interfaces exist. The idea is to make the actual calculation algorithm exchangeable whereas the code used in an applications shall remain unchanged. The models are technically bi-functions which consume a Collection of equation objects (<T extends Orientable>) and a Dimension instance. The Dimension instance holds the information how many X,Y locations exist and how the data is oriented (e.g. 1D one-dimensional, either X or Y or 2D two-dimensional X and Y). Using the equations and the dimensional information any kind or matrix based system can be configured.

Models and Transforms Interfaces

Examples

There are some demos available, how this library is supposed to be used:

The class net.raumzeitfalle.registration.examples.Demo is used to define all examples. This template allows it, to configure and parameterize the evaluation process as needed.

The following example code shows, how alignment on 4 selected locations works, with info only locations being removed. First order (scale/ortho) will be calculated on all locations. To calculate first order on selected locations, Alignments.SCANNER_SELECTED must be used.

    
    /* STEP 1, load displacements from file (or any other source)
     *
     * The CSV file may look like:
     * "refx","refy","posx","posy","diffx","diffy","type"
     * 10980.0,9012.5,10980.014331404400,9012.481628831100,0.014331404400,-0.018371168900,"ALIGN"
     * 10980.0,73512.5,10980.009388937700,73512.484174799200,0.009388937700,-0.015825200800,"REG_MARK"
     * 10980.0,143387.5,10980.004598393400,143387.490394277000,0.004598393400,-0.009605722700,"ALIGN"
     * ....
     * 146975.0,14925.0,146975.030283248000,NaN,0.030283248900,NaN,"INFO_ONLY"
     * 
     * All values are stored with the same unit, in this example all columns consist
     * of values in microns. The values in columns (diffx,diffy) are not used.
     * In case of one-dimensionality or missing values, NaN can be used.
     * 
     */

    List<Displacement> displacements = new FileLoader().load(Paths.get("Demo-4Point.csv"));
        
    /*
     * 
     * Each Displacement consists of a design location (x,y) and the actual displaced
     * location (xd,yd). By default, each Displacement is of type REG, but depending
     * on declaration in CSV file, a different DisplacementClass can be assigned.
     * The DisplacementClass allows to create simple predicates to select Displacmemt  
     * instances for different operations.
     *
     */
    

    // STEP 2, perform site selection
    Predicate<Displacement> allSites = d->true;
     
    SiteSelection selection = SiteSelection
                        .forAlignment(d -> d.isOfType(DisplacementClass.ALIGN))
                        .forCalculation(allSites)
                        .forRemoval(d->d.isOfType(DisplacementClass.INFO_ONLY));
    
    // STEP 3, parametrize evaluation model 
    FirstOrderSetup setup = FirstOrderSetup
                        .usingAlignment(Alignments.SELECTED)
                        .withCompensations(Compensations.SCALE, Compensations.ORTHO)
                        .withSiteSelection(selection);

    // STEP 4, perform correction and calculate results
    FirstOrderResult result = FirstOrderCorrection.using(displacements, setup);
    Collection<Displacement> results = result.getDisplacements();

    /* 
     *  Alternatively:
     *
     *  FirstOrderCorrection correction = new FirstOrderCorrection();
     *  results = correction.apply(displacements, setup).getDisplacements();
     * 
     *  As FirstOrderCorrection is a function, .andThen(...) and .compose(...) 
     *  can be used as well. 
     *
     */  
    
    // STEP 5, print results
        
    // Now print results before correction
    DisplacementSummary uncorrectedSummary = Displacement.summarize(displacements, selection.getCalculation());
    System.out.println(uncorrectedSummary);
        
    // after correction
    DisplacementSummary correctedSummary = Displacement.summarize(results, selection.getCalculation());
    System.out.println(correctedSummary);
        
    // now also print residual first order and alignment
    RigidTransform correctedAlignment = result.getAlignment();
    System.out.println(correctedAlignment);
        
    AffineTransform correctedFirstOrder = result.getFirstOrder();
    System.out.println(correctedFirstOrder);

Transform types

Symbol Description
+ is directly calculated by model
o can be approximated from results
sx/sy anisotropic scaling (scale x/y)
mag magnification, isotropic scaling (mag = average(sx,sy))
ox/oy anisotropic rotation (shearing or non-orthogonality, ortho x/y)
ortho isotropic non-orthogonality (ortho = oy - ox)
rot isotropic rotation
tx/ty translation in x/y direction
Transform tx ty sx sy mag ox oy ortho rot
Rigid + +             +
Affine + + + + o + + + o
Similarity + +     +     o +
Non-Uniform Similarity + + + + o     o +

Cases

#1 common case, references and readings in 2D (X,Y)

2D references with readings in XY

Direction Refs Readings
X (count) > 1 > 1
Y (count) > 1 > 1

#2 special case, references 2D, readings 1D (X)

2D references with readings in X

Direction Refs Readings
X (count) > 1 > 1
Y (count) > 1 = 0

#3 special case, references 2D, readings 1D (Y)

2D references with readings in Y

Direction Refs Readings
X (count) > 1 = 0
Y (count) > 1 > 1

#4 common case, references in 2D, most readings (X,Y), some readings (X or Y)

2D references with partially missing X or Y

Direction Refs Readings
X (count) > 1 > 1
Y (count) > 1 > 1

#5 special case, references along horizontal line, readings in 2D (X,Y)

references along horizontal line (1D) with X and Y

Direction Refs Readings
X (count) > 1 > 1
Y (count) = 1 > 1

#6 special case, references along vertical line, readings in 2D (X,Y)

references along vertical line (1D) with X and Y

Direction Refs Readings
X (count) = 1 > 1
Y (count) > 1 > 1

#7 special case, references along horizontal line, readings in 1D (X)

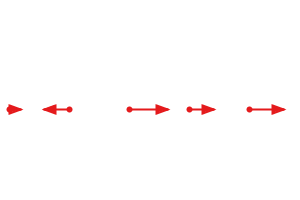
references along horizontal line (1D) with X only

Direction Refs Readings
X (count) > 1 > 1
Y (count) = 1 = 0

#8 special case, references along horizontal line, readings in 1D (Y)

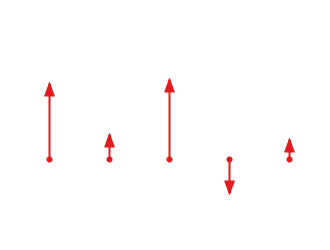
references along horizontal line (1D) with Y only

Direction Refs Readings
X (count) > 1 = 0
Y (count) = 1 > 1

#9 special case, references along vertical line, readings in 1D (X)

#10 special case, references along vertical line, readings in 1D (Y)

#11 special case, only one reference position, readings in (X and Y) or (X or Y)

references on one single location, partially with X and Y, some XY

References for further reading

License

Apache License, Version 2.0

Copyright 2019 Oliver Löffler, Raumzeitfalle.net

Licensed under the Apache License, Version 2.0 (the “License”); you may not use this file except in compliance with the License. You may obtain a copy of the License at

   http://www.apache.org/licenses/LICENSE-2.0

Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an “AS IS” BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.

Attributions, external libraries used with their licenses

This project makes use of NIST.gov JAMA library. JAMA is public domain, see: https://math.nist.gov/javanumerics/jama/#license.

Also this project uses LA4J library, which also follows Apache 2.0 license. See http://la4j.org for details, sources can be found at https://github.com/vkostyukov/la4j.